一般社団法人世界メッシュ研究所

文档

关于世界网格编码及世界网格统计的文档

网格统计的有效利用与面向世界网格统计的延伸

1 简介

地域网格编码[1]如今在日本国内网格统计的计算中已经必不可少。日本总务省统计局通过e-Stat[2]将国势调查等政府统计数据网格化后，作为政府开放数据公开在“地图上看数据（统计GIS）”[3]上。并且，日本国土交通省国土政策局国土情报科，也将从国土交通省累积的位置统计调查中得到的网格统计数据作为国土数值信息进行了公开[4]。另外，地域网格统计在灾害发生时估算受灾范围和受灾规模，企业在新地区开设店铺时估算盈利状况，制定公共政策所需费用的预算等场合均得到了应用。

本文中将在解说地域网格统计的同时，关于笔者在统计2015年9月号上刊登的《大数据时代中必要的标准化》中所提及的从地域网格编码到世界网格编码的扩展方法进行概述。最后，对世界网格编码作为世界标准规格被使用时的应用前景进行了讨论。

2 地域网格编码

在进入正题之前，先概论一下关于地域网格统计的历史。地域网格统计是被称为“网格(grid)法”的统计方法之一。是一种将空间切割为某种区划（grid或者mesh），利用单独数据的区划属性其各个单项进行统计，从而制作依赖于空间关系的统计数据的方法。

在计算地域网格统计时，首先需要对区划进行定义。建立通用的区划方法将使得不同组织为了不同目的所收集制作的地域网格统计数据之间可以进行比较与结合。

本网格编码（meshcode）在1973年7月12日由日本总理府统计局提出，此后在1976年1月作为日本工业规格JIS X0410被设立为标准，如今在日本国内已经得到了广泛的应用。

在地域网格统计中所使用的网格编码，根据区域划分的大小分为1级网格（80km*80km），2级网格（10km*10km），3级网格（1km*1km）（更小的划分还有4级网格（500m*500m），5级网格（250m*250m），6级网格（125m*125m））。

3级网格编码表现为一列8位的数字，其前4位为1级网格编码，前6位为2级网格编码，从而对应到更大的网格。1级网格编码下的1区划为纬度差40分，经度差1度。在日本附近一边的长度约为80km。2级网格编码下的1区划是将1级网格编码的1区划在经度与纬度的方向各自进行了8等分后，纬度差5分，经度差7分30秒，对应一边长度约为10km的区域。3级网格编码下的1区划是将2级网格编码在经度与纬度的方向各自进行了10等分后，纬度差30秒，经度差45秒，对应一边长度为1km的区域。

设$(\mbox{纬度},\mbox{经度})=(\mbox{latitude}, \mbox{longitude})$, 则表示由该经纬度所确定地点所属的3级网格的地域网格编码可由如下算式计算获得。[1].
\begin{equation}
\mbox{grid square code} = pu qv rw.
\end{equation}
此处，整数值变量$p,u,q,v,r,w$的计算如下。
\begin{equation}
\left\{
\begin{array}{lcl}
\lfloor \mbox{latitude} \times 60 \div 40 \rfloor = p \quad (\mbox{$p$ is two digits.}),
%\label{eq:expression:p}
\\
a = (\mbox{latitude} \times 60 \div 40 – p) \times 40,
%\label{eq:expression:a}
\\
\lfloor a \div 5 \rfloor = q \quad (\mbox{$q$ is one digit.}),
%\label{eq:expression:q}
\\
b = (a \div 5 – q) \times 5,
%\label{eq:expression:b}
\\
\lfloor b \times 60 \div 30 \rfloor = r \quad (\mbox{$r$ is one digit.}),
%\label{eq:expression:r}
\\
c = (b \times 60 \div 30 – r) \times 30,
%\label{eq:expression:c}
\\
\lfloor \mbox{longitude} – 100 \rfloor = u \quad (\mbox{$u$ is two digits.}),
%\label{eq:expression:u}
\\
f = \mbox{longitude} – 100 – u,
%\label{eq:expression:f}
\\
\lfloor f \times 60 \div 7.5 \rfloor = v \quad (\mbox{$v$ is one digit.}),
%\label{eq:expression:v}
\\
g = (f \times 60 \div 7.5 – v) \times 7.5,
%\label{eq:expression:g}
\\
\lfloor g \times 60 \div 45 \rfloor = w \quad (\mbox{$w$ is one digit.}),
%\label{eq:expression:w}
\\
h = (g \times 60 \div 45 – w) \times 45,
%\label{eq:expression:h}
\end{array}
\right.
\end{equation}
同样反过来, 从3级网格编码$pu qv rw$也可以计算出该网格编码西南角的纬度$\mbox{latitude}$与经度$\mbox{longitude}$。
\begin{equation}
\left\{
\begin{array}{lcl}
\mbox{latitude} &=& p \times 40 \ \div 60 + q \times 5 \div 60 + r \times 30 \div 3600, \\
\mbox{longitude} &=& 100 + u + v \times 7.5 \div 60 + w \times 45 \div 3600.
\end{array}
\right.
\end{equation}

通过网格编码，可以得到将日本国土依照经度与纬度划分为区域（网格）的唯一空间表现数列。然而，由于该网格编码的定义仅限于日本国内的空间位置，在形式上，定义域范围为东经100度到180度，北纬0度到66.66度（虽然在日本的临近国家与地区，如韩国台湾等地JIS X0410也可以直接使用。但是就笔者所知，在日本以外的邻近地区并没有利用JIS X0410制作地域网格统计。）因此，网格编码尚未覆盖全球所有地方。在下一节中将讨论JIS X0410扩展到地球全体的方法。

3 JIS X041向世界网格编码的扩展

由于JIS X0410是以妥善划分日本周边地区为目的而设计的网格编码，被网格定义的点$(\mbox{latitude},\mbox{longitude})$的定义域被限制为$0^{\circ} \leq \mbox{latitude} < 66.66^{\circ}$,
$100^{\circ} \leq \mbox{longitude} < 180^{\circ}$.

因此，仅仅依靠JIS X0410则难以表现日本以外地区的空间。为了克服这个问题，需要考虑如何将JIS X0410的网格编码的计算方法扩展到$-90^{\circ} < \mbox{latitude} < 90^{\circ}$, $-180^{\circ} < \mbox{longitude} < 180^{\circ}$.

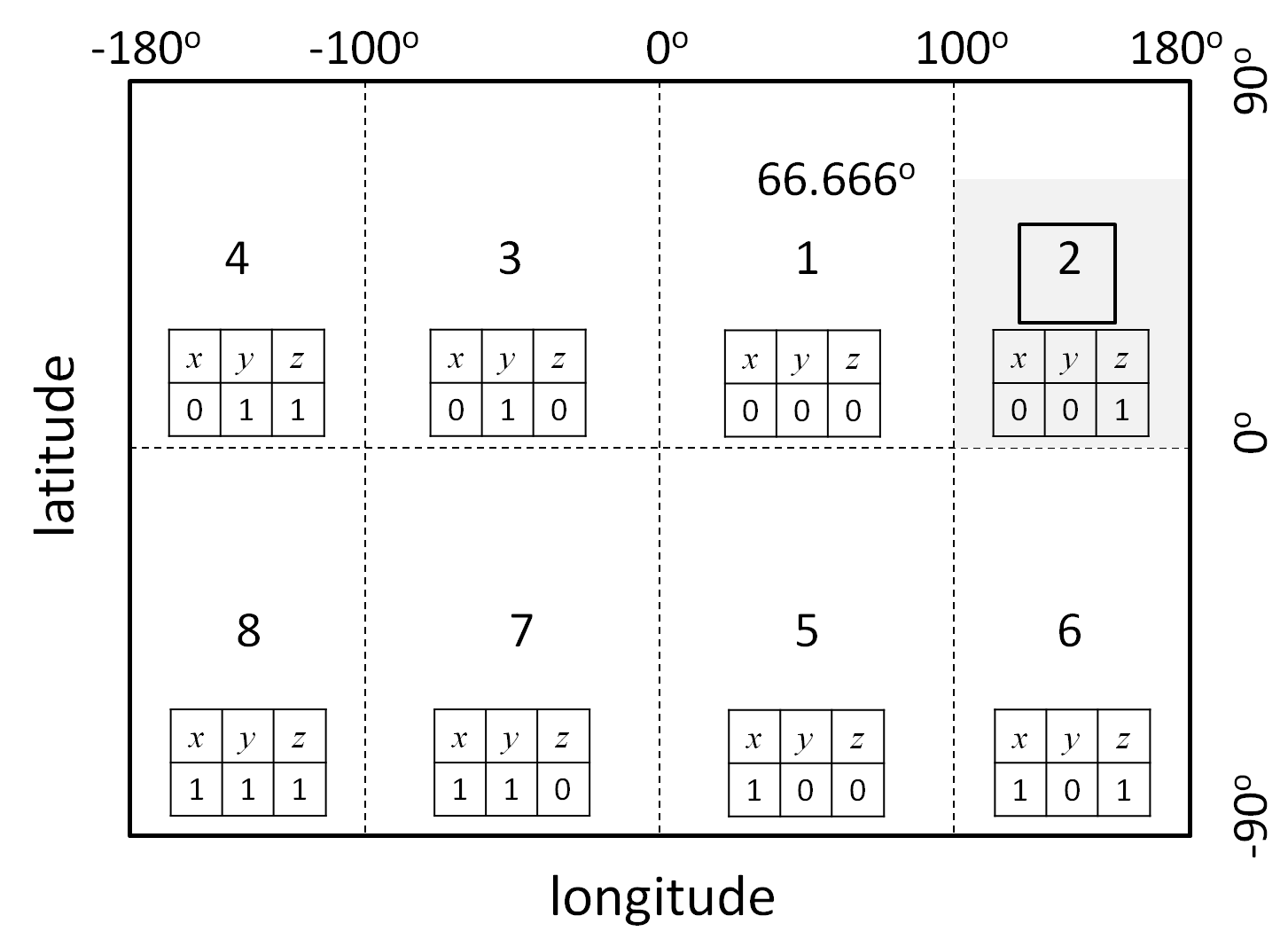
网格编码的世界扩展及与0级网格编码的关系.

如图1所示, 全世界范围内纬度与经度的定义域$-90 \leq \mbox{latitude} < 90^{\circ}$, $-180^{\circ} \leq \mbox{longitude} < 180^{\circ}$中，仅有阴影所示的部分为JIS X0410的网格编码的定义域$0^{\circ} \leq \mbox{latitude} < 66.66^{\circ}$, $100^{\circ} \leq \mbox{longitude} < 180^{\circ}$.

在$0^{\circ} \leq \mbox{latitude} < 90^{\circ}$, $100^{\circ} \leq \mbox{longitude} < 180^{\circ}$中, $p$既可能是3位也可能是1位, $u$也可能是1位. 因此, 首先, 关于1级网格编码中对应纬度的$p$从2 digits扩展至3 digits. 如果$p$在10以下，则在前边添上00补成3 digits. 如果$p$在10以上100以下，则在前边添上0补成3 digits. 并且，$u$在10以下时也同样在前边添上0补成2 digits. 接下来, 依照如下的条件来考虑将世界进行划分。

1. 将纬度区分为南纬和北纬两个状态。因此，添加上表示北纬($x=0$)与南纬($x=1$)的1bit.
2. 将经度区分为东经和西经两个状态。因此, 添加上表示东经($y=0$)与西经($y=1$)的1bit.
3. 使用1bit来表示经度的绝对值在100$^{\circ}$以下和100$^{\circ}$以上2个状态，设$|\mbox{longitude}| \geq 100^{\circ}$($z=1$)，$|\mbox{longitude}|<100^{\circ}$($z=0$).

包含现有的JIS X0410在内，一共有8个这样的区域(参考图1). 因此，将$xyz$3bit转换为10进制之后全体加1，从而得到一个1位（1到8）的数值作为扩展编码。通过这个方法，理论上仅仅按照JIS X0410计算网格编码，并且赋予一个1到8之间的1位扩展编码，就可以对扩展到世界范围的网格编码进行定义。表1总结了1到8 的扩展编码所对应的地球上的领域。像这样定义的从1到8的1位扩张编码从方便上被称为0级网格编码。

已知$xyz$的时候, 0级网格编码$o$的计算方法是,
\begin{equation}
o=2^2 x + 2 y + z + 1.
\end{equation}
. 另外，当已知0级网格编码$o$(1～8)的时候，$xyz$可由如下计算获得。
\begin{eqnarray}
z &=& (o – 1) \mbox{ mod } 2, \\
y &=& ((o – z – 1) \div 2) \mbox{ mod } 2, \\
x &=& (o – 2 \times y – z – 1) \div 4,
\end{eqnarray}

当已知由纬度$\mbox{latitude}$和经度$\mbox{longitude}$表示的位置信息(WGS84)的时候，各级网格编码的整数值的计算公式可以扩展如下。

1级网格编码
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0u & (p < 10, u < 10) \\
o0p0u & (10 \leq p < 100, u < 10) \\
op0u & (p \geq 100, u < 10) \\
o00pu & (p < 10, u \geq 10) \\
o0pu & (10 \leq p < 100, u \geq 10) \\
opu & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}

2级网格编码
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0uqv & (p < 10, u < 10) \\
o0p0uqv & (10 \leq p < 100, u < 10) \\
op0uqv & (p \geq 100, u < 10) \\
o00puqv & (p < 10, u \geq 10) \\
o0puqv & (10 \leq p < 100, u \geq 10) \\
opuqv & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}

3级网格编码
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0uqvrw & (p < 10, u < 10) \\
o0p0uqvrw & (10 \leq p < 100, u < 10) \\
op0uqvrw & (p \geq 100, u < 10) \\
o00puqvrw & (p < 10, u \geq 10) \\
o0puqvrw & (10 \leq p < 100, u \geq 10) \\
opuqvrw & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}

4级网格编码
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0uqvrws_2 & (p < 10, u < 10) \\
o0p0uqvrws_2 & (10 \leq p < 100, u < 10) \\
op0uqvrws_2 & (p \geq 100, u < 10) \\
o00puqvrws_2 & (p < 10, u \geq 10) \\
o0puqvrws_2 & (10 \leq p < 100, u \geq 10) \\
opuqvrws_2 & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}

5级网格编码
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0uqvrws_2s_4 & (p < 10, u < 10) \\
o0p0uqvrws_2s_4 & (10 \leq p < 100, u < 10) \\
op0uqvrws_2s_4 & (p \geq 100, u < 10) \\
o00puqvrws_2s_4 & (p < 10, u \geq 10) \\
o0puqvrws_2s_4 & (10 \leq p < 100, u \geq 10) \\
opuqvrws_2s_4 & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}

6级网格编码
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0uqvrws_2s_4s_8 & (p < 10, u < 10) \\
o0p0uqvrws_2s_4s_8 & (10 \leq p < 100, u < 10) \\
op0uqvrws_2s_4s_8 & (p \geq 100, u < 10) \\
o00puqvrws_2s_4s_8 & (p < 10, u \geq 10) \\
o0puqvrws_2s_4s_8 & (10 \leq p < 100, u \geq 10) \\
opuqvrws_2s_4s_8 & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}

其中，各整数值可由如下计算获得。
\begin{equation}
\left\{
\begin{array}{l}
p: = \lfloor (1-2x)\mbox{latitude} \times 60 \div 40 \rfloor \quad (\mbox{$p$ is two or three digits}),
\\
a := \bigl\{(1-2x)\mbox{latitude} \times 60 \div 40 – p\bigr\} \times 40, \\
q := \lfloor a \div 5 \rfloor \quad (\mbox{$q$ is one digit}),
\\
b := (a \div 5 – q) \times 5,
\\
r := \lfloor b \times 60 \div 30 \rfloor \quad (\mbox{$r$ is one digit}),
\\
c := (b \times 60 \div 30 – r) \times 30,
\\
s_{2u} := \lfloor c/15 \rfloor \quad (\mbox{$s_{2u}$ is one digit}),
\\
d := (s_{2u}/15-s_{2u}) \times 15,
\\
s_{4u} := \lfloor d/7.5 \rfloor \quad (\mbox{$s_{4u}$ is one digit}),
\\
e := (d/7.5-s_{4u}) \times 7.5,
\\
s_{8u} := \lfloor e/3.75 \rfloor \quad (\mbox{$s_{8u}$ is one digit}),
\\
u := \lfloor (1-2y)\mbox{longitude} – 100z \rfloor \quad (\mbox{$u$ is one or two digits}),
\\
f := (1-2y)\mbox{longitude} – 100z – u,
\\
v := \lfloor f \times 60 \div 7.5 \rfloor \quad (\mbox{$v$ is one digit}),
\\
g := (f \times 60 \div 7.5 – v) \times 7.5,
\\
w := \lfloor g \times 60 \div 45 \rfloor \quad (\mbox{$w$ is one digit}),
\\
h := (g \times 60 \div 45 – w) \times 45,
\\
s_{2l} := \lfloor h/22.5 \rfloor \quad (\mbox{$s_{2l}$ is one digit}),
\\
i := (s_{2l}/22.5-s_{2l}) \times 22.5,
\\
s_{4l} := \lfloor i/11.25 \rfloor \quad (\mbox{$s_{4l}$ is one digit}),
\\
j := (s_{4l}/11.25-s_{4l}) \times 11.25,
\\
s_{8l} := \lfloor j/5.625 \rfloor \quad (\mbox{$s_{8l}$ is one digit}),
\\
s_2 := s_{2u} \times 2+s_{2l}+1 \quad (\mbox{$s_{2}$ is one digit}),
\\
s_4 := s_{4u} \times 2+s_{4l}+1 \quad (\mbox{$s_{4}$ is one digit}),
\\
s_8 := s_{8u} \times 2+s_{8l}+1 \quad (\mbox{$s_{8}$ is one digit})
\end{array}
\right..
\end{equation}

反过来，已知1级网格编码 $opu$ ($o$(1 digit), $p$(3 digits), $u$(2 digits))的时候，表示其西北角位置的纬度$\mbox{latitude}$和经度$\mbox{longitude}$可由
\begin{eqnarray}
\mbox{latitude} &=& (1-2x) \bigl\{(p-x+1) \times 40 \ \div 60 \bigr\}, \\
\mbox{longitude} &=& (1-2y) (100 \times z + u+y ).
\end{eqnarray}
计算得出。

已知2级网格编码 $opuqv$ ($o$(1 digit), $p$(3 digits), $u$(2 digits), $q$(1 digit), $v$(1 digit))的时候，表示其西北角位置的纬度$\mbox{latitude}$和经度$\mbox{longitude}$可由
\begin{eqnarray}
\nonumber
\mbox{latitude} &=& (1-2x) \bigl\{p \times 40 \ \div 60 \\
&+& (q-x+1) \times 5 \div 60 \bigr\}, \\
\label{eq:expression2:latitude-mesh-2}
\mbox{longitude} &=& (1-2y) \bigl(100 \times z + u \\
\nonumber
&+& (v+y) \times 7.5 \div 60 \bigr).
\label{eq:expression2:longitude-mesh-2}
\end{eqnarray}
计算得出。

已知3级网格编码 $opuqvrw$ ($o$(1 digit), $p$(3 digits), $u$(2 digits), $q$(1 digit), $v$(1 digit), $r$(1 digit), $w$(1 digit)) 的时候，表示其西北角位置的纬度$\mbox{latitude}$和经度$\mbox{longitude}$可由
\begin{eqnarray}
\nonumber
\mbox{latitude} &=& (1-2x) \bigl(p \times 40 \ \div 60 + q \times 5 \div
60 \\
&+& (r-x+1) \times 30 \div 3600 \bigr), \\
\label{eq:expression2:latitude-mesh-3}
\nonumber
\mbox{longitude} &=& (1-2y) \bigl(100 \times z + u + v \times 7.5 \div 60
\\
&+& (w+y) \times 45 \div 3600 \bigr).
\label{eq:expression2:longitude-mesh-3}
\end{eqnarray}
计算得出。

已知4级网格编码 $opuqvrws_2$ ($o$(1 digit), $p$(3 digits), $u$(2 digits), $q$(1 digit), $v$(1 digit), $r$(1 digit), $w$(1 digit), $s_2$(1digit)) 的时候，表示其西北角位置的纬度$\mbox{latitude}$和经度$\mbox{longitude}$可由
\begin{eqnarray}
\nonumber
\mbox{latitude} &=& (1-2x) \bigl(p \times 40 \ \div 60 + q \times 5 \div
60 \\
\nonumber
&+& (r-x+1) \times 30 \div 3600 \\
&+& \lfloor (s_2-1)/2 \rfloor + x-1) \times 15 \div 3600 \bigr), \\
\label{eq:expression2:latitude-mesh-4}
\nonumber
\mbox{longitude} &=& (1-2y) \bigl(100 \times z + u + v \times 7.5 \div 60
\\
\nonumber
&+& (w+y) \times 45 \div 3600 \\
&+& (((s_2-1) \mbox{ mod } 2) – y) \times 22.5 \div 3600 \bigr).
\label{eq:expression2:longitude-mesh-4}
\end{eqnarray}
计算得出。

已知5级网格编码 $opuqvrws_2s_4$ ($o$(1 digit), $p$(3 digits), $u$(2 digits), $q$(1 digit), $v$(1 digit), $r$(1 digit), $w$(1 digit), $s_2$(1 digit), $s_4$(1 digit))的时候，表示其西北角位置的纬度$\mbox{latitude}$和经度$\mbox{longitude}$可由
\begin{eqnarray}
\nonumber
\mbox{latitude} &=& (1-2x) \bigl(p \times 40 \ \div 60 + q \times 5 \div
60 \\
\nonumber
&+& (r-x+1) \times 30 \div 3600 \\
\nonumber
&+& \lfloor (s_2-1)/2 \rfloor + x-1)) \times 15 \div 3600 \\
&+& \lfloor (s_4-1)/2 \rfloor + x-1)) \times 7.5 \div 3600\bigr), \\
\label{eq:expression2:latitude-mesh-5}
\nonumber
\mbox{longitude} &=& (1-2y) \bigl(100 \times z + u + v \times 7.5 \div 60
\\
\nonumber
&+& (w+y) \times 45 \div 3600 \\
\nonumber
&+& (((s_2-1) \mbox{ mod } 2) – y) \times 22.5 \div 3600 \\
&+& (((s_4-1) \mbox{ mod } 2) – y) \times 11.25 \div 3600 \bigr).
\label{eq:expression2:longitude-mesh-5}
\end{eqnarray}
计算得出。

已知6级网格编码 $opuqvrws_2s_4s_8$ ($o$(1 digit), $p$(3 digits), $u$(2 digits), $q$(1 digit), $v$(1 digit), $r$(1 digit), $w$(1 digit), $s_2$(1 digit), $s_4$(1 digit), $s_8$(1 digit)) 的时候，表示其西北角位置的纬度$\mbox{latitude}$和经度$\mbox{longitude}$可由
\begin{eqnarray}
\nonumber
\mbox{latitude} &=& (1-2x) \bigl(p \times 40 \ \div 60 + q \times 5 \div
60 \\
\nonumber
&+& (r-x+1) \times 30 \div 3600 \\
\nonumber
&+& \lfloor (s_2-1)/2 \rfloor + x-1)) \times 15 \div 3600 \\
\nonumber
&+& \lfloor (s_4-1)/2 \rfloor + x-1)) \times 7.5 \div 3600 \\
&+& \lfloor (s_8-1)/2 \rfloor + x-1)) \times 3.75 \div 3600 \bigr), \\
\label{eq:expression2:latitude-mesh-6}
\nonumber
\mbox{longitude} &=& (1-2y) \bigl(100 \times z + u + v \times 7.5 \div 60
\\
\nonumber
&+& (w+y) \times 45 \div 3600 \\
\nonumber
&+& (((s_2-1) \mbox{ mod } 2) – y) \times 22.5 \div 3600 \\
\nonumber
&+& (((s_4-1) \mbox{ mod } 2) – y) \times 11.25 \div 3600 \\
&+& (((s_8-1) \mbox{ mod } 2) – y) \times 5.625 \div 3600 \bigr).
\label{eq:expression2:longitude-mesh-6}
\end{eqnarray}
计算得出。

将JIS X0410扩展到世界范围的扩展编码（0级网格编码）的定义.

$x$: 纬度 $y$: 经度 $z$: 经度的范围 $x|y|z$ 10进制表示
$0$: 北纬 ($\mbox{latitude} > 0^{\circ}$) $0$: 东经 ($\mbox{longitude} > 0^{\circ}$) $0$: $|\mbox{longitude}| < 100^{\circ}$ $0|0|0$ $1$
$0$: 北纬 ($\mbox{latitude} > 0^{\circ}$) $0$: 东经 ($\mbox{longitude} > 0^{\circ}$) $1$: $|\mbox{longitude}| \geq 100^{\circ}$ $0|0|1$ $2$
$0$: 北纬 ($\mbox{latitude} > 0^{\circ}$) $1$: 西经 ($\mbox{longitude} < 0^{\circ}$) $0$: $|\mbox{longitude}| < 100^{\circ}$ $0|1|0$ $3$
$0$: 北纬 ($\mbox{latitude} > 0^{\circ}$) $1$: 西经 ($\mbox{longitude} < 0^{\circ}$) $1$: $|\mbox{longitude}| \geq 100^{\circ}$ $0|1|1$ $4$
$1$: 南纬 ($\mbox{latitude} < 0^{\circ}$) $0$: 东经 ($\mbox{longitude} > 0^{\circ}$) $0$: $|\mbox{longitude}| < 100^{\circ}$ $1|0|0$ $5$
$1$: 南纬 ($\mbox{latitude} < 0^{\circ}$) $0$: 东经 ($\mbox{longitude} > 0^{\circ}$) $1$: $|\mbox{longitude}| \geq 100^{\circ}$ $1|0|1$ $6$
$1$: 南纬 ($\mbox{latitude} < 0^{\circ}$) $1$: 西经 ($\mbox{longitude} < 0^{\circ}$) $0$: $|\mbox{longitude}| < 100^{\circ}$ $1|1|0$ $7$
$1$: 南纬 ($\mbox{latitude} < 0^{\circ}$) $1$: 西经 ($\mbox{longitude} < 0^{\circ}$) $1$: $|\mbox{longitude}| \geq 100^{\circ}$ $1|1|1$ $8$

像这样定义之后，在迄今依照JIS X0410定义的网格编码前添加上0级网格编码2和1级网格编码0后即可扩展为世界网格编码。

在这里介绍如何笔者等提出的世界网格编码的试行提案通过R语言实装[10]。在库中定义了如下函数。

    • 输出世界3级网格四角的纬度和经度
meshcode_to_latlong_grid(meshcode)
    • 输出世界3级网格西北角的纬度和经度
meshcode_to_latlong_NW(meshcode)
    • 输出世界3级网格西南角的纬度和经度
meshcode_to_latlong_SW(meshcode)
    • 输出世界3级网格东北角的纬度和经度
meshcode_to_latlong_NE(meshcode)
    • 输出世界3级网格东南角的纬度和经度
meshcode_to_latlong_SE(meshcode)
    • 输出位置信息（纬度和经度）以及包含该位置的世界3级网格编码
cal_meshcode(latitude,longitude)

地球是半径$r$大约为6,371km的球体，其表面积$S$大约为$S = 510,100,000$ km$^2$. 覆盖全球的1级网格的总数为 360 $\times$ 180 $\times$ 3/2 = 97,200. 2级网格的总数为1级网格的64倍，因此覆盖全球的2级网格的总数为 6,220,800. 3级网格的总数为2级网格的100倍，因此覆盖全球的3级网格的总数为 622,080,000. 4级网格的总数是3级网格的4倍，因此4级网格的总数为2,488,320,000. 5级网格的总数手机4级网格的4倍，因此5级网格的总数为9,953,280,000. 6级网格的总数是5级网格的4倍，因此6级网格的总数为39,813,120,000.

另外，地球上陆地面积约占全球的29.2998%，各级世界网格的总数以及陆地上世界网格的总数分别总结如下表。


覆盖全球的世界网格的总数和陆地上世界网格的总数.

世界网格级别 覆盖全球的网格总数 陆地上网格总数
1级网格 97,200 28,383
2级网格 6,220,800 2,838,220
3级网格 622,080,000 181,646,116
4级网格 2,488,320,000 726,584,463
5级网格 9,953,280,000 2,906,337,853
6级网格 39,813,120,000 11,625,351,413

 

[1] 日本总务省统计局 地域网格统计的概要 [10 August 2015] http://www.stat.go.jp/data/mesh/gaiyou.htm
[2] e-Stat https://www.e-stat.go.jp/SG1/estat/eStatTopPortal.do
[3] 地图上看数据（统计GIS）https://www.e-stat.go.jp/SG1/estat/toukeiChiri.do?method=init
[4] 日本国土交通省国土政策局国土情报科 http://www.mlit.go.jp/kokudoseisaku/kokudojoho.html
[5] 佐藤彰洋, 椿广计, 在大数据时代需要的标准化, 统计, 2015年9月号, pp.32–38.
[6] 关于日本国土实况综合统计的开发整备的研究报告（昭和46年）发行：日本总理府统计局
[7] 日本国土交通省观光厅 http://www.mlit.go.jp/kankocho/
[8] 住宿旅行统计调查 http://www.mlit.go.jp/kankocho/siryou/toukei/shukuhakutoukei.html
[9] R语言计算世界网格编码用的库. https://www.fttsus.jp/worldmesh/library.html
[10] Ordnance Survey National Grid reference system http://www.ordnancesurvey.co.uk/support/the-national-grid.html