一般社団法人世界メッシュ研究所

ドキュメント

世界メッシュコードおよび世界メッシュ統計に関するドキュメント

公表資料

検討会公開資料

研究会公開ドキュメント

メッシュ統計の利活用と世界メッシュ統計への拡張

1 はじめに

地域メッシュコード[1]は現在国内メッシュ統計を計算する上でなくてはならないものとなっている. 総務省統計局はe-Stat[2]を通じて, 地図で見る統計(統計GIS)[3]から総務省統計局国勢調査やセンサスなどの政府統計をメッシュデータ化し政府オープンデータとして公開している. また, 国土交通省国土政策局国土情報課は国土数値情報として, 国土交通省で蓄積されている位置付き統計調査をメッシュ統計として公表している[4]. 更に, 地域メッシュ統計は, 災害時の被害範囲や被害規模の試算, 企業の新規出店地域での売上試算, 公共政策の需要見積りなどに応用されるようになっている.

このように地域メッシュ統計が我が国で広く作成され, 利用されるようになった背景には, 我が国における地域メッシュ統計制度の策定から利用に至る長い歴史が存在している.

本稿では, 地域メッシュコードについて解説し, 著者らが統計2015年9月号で発表した「ビッグデータ時代に必要な標準化」[5]で示した地域メッシュコードの世界メッシュコードへの拡張方法について概説する. 更に, 世界メッシュコードが世界標準規格として利用できるようになった場合の応用の可能性について議論する.

2 地域メッシュコード

本論に入る前に, 地域メッシュ統計の歴史について概観したい. 地域メッシュ統計とは「グリッド法」と呼ばれる統計集計方法のひとつである. 空間をある区画（グリッドまたはメッシュと呼ぶ）に分割し, 個票データの区画属性を利用して, 個票データの各項目を集計することにより, 空間に依存した統計を作り出す方法である.

地域メッシュ統計を算出するためには, 区画の定義が必須である. 更に, 区画を共通としておくことにより, 異なる目的で異なる組織が集計した地域メッシュ統計を比較, 結合することが可能となる.

日本においてはメッシュ統計を計算する上で重要となる区画はメッシュコードと呼ばれる区画と一意に対応する数列により日本産業規格（旧日本工業規格）(JIS)として標準化がなされている.

このメッシュコードは, 1973年7月12日に総理府統計局により提唱され, その後1976年1月にJIS X0410として日本産業規格として標準化がなされ, 現在国内で広く利用されるようになっている. 雑誌統計においては, 1974年5月～1976年9月にかけて連載講座として「地域メッシュ統計講座」がある. 様々なグリッド定義について比較検討がなされ, 現在のJIS X0410で標準化されているメッシュコードのエンコードが採用されるに至った経緯を連載から読み取ることができる.

このメッシュコード策定の経緯を「国土実態総合統計の開発・整備に関する研究報告（昭和46年）発行：総理府統計局」[6]より紐解いてみよう.

1970年代当時の統計の地域表章単位は市区町村単位によるものであったが, 市町村合併により, 市区町村間の属性に大きな歪みが生じ, 比較しても無意味な結果となり, また, 市区町村の行政区域がたびたび変動することで時系列的統計の作成が困難であった. 更に, 数個の市区町村にまたがった単位が必要となる広域的行政には, 市区町村単位の統計では, 利用上不便であった. このような既存の地域統計の不備を補うために, 既存統計を有効に活用し, 任意の地域について各統計の総合的な利用をはかることを目的として地域メッシュ統計を活用することとなった.

このような問題点を考慮し, 総理府統計局（当時）は昭和44年度総理府統計局「国土実態総合統計」において, 地域メッシュ統計を試験的に作成した. このとき, 国勢調査, 事業所統計調査, 住宅統計調査がこの対象となった. 更に, 建設省国土地理院（当時）は昭和44年度建設省国土地理院土地利用関係データの「メッシュマップ」を試験的に研究した. また, 総理府経済企画庁総合開発局は（当時）は昭和45年度経済企画庁「国土実態総合調査」において, 地域メッシュによる土地条件・気象条件など自然的現象を中心としたメッシュ・データのためのパイロット調査を行った.

その後, このような動きは, 省庁を越えて行われるようになった. 例えば, 建設省計画局(当時）は「メッシュデータの地域計画等への利用方法の研究」防衛庁(当時）は「地域メッシュのデータ収集」, 北海道開発庁（当時）は「地域メッシュのデータ収集」が行われるようになった. このような, 各省庁における地域メッシュデータの作成の動きに促され, 行政管理庁では, 地域メッシュデータの相互利用という観点から標準メッシュの設定とそのコーディングについて, 統計審議会に諮問するに至った. これにより, 統計審議会では, メッシュの部会を設け, 総理府, 建設省, 経済企画庁等の間ですでに合意に達していた経緯度法による地域メッシュの設定およびコーディングの案を標準として採用することで意見が一致し, 昭和44年12月各省庁が地域メッシュによる統計を作成する場合には, 標準メッシュによることを要する旨が統計審議会会長から行政管理長官に答申された. そして, 昭和51年(1976)に, 日本工業規格（現在の日本産業規格）としてJIS X0410として標準化がなされることとなった.

地域メッシュ統計で用いられるメッシュコードは, その区画の大きさからそれぞれ1次メッシュ(80km四方), 2次メッシュ(10km四方), 3次メッシュ(1km四方)と呼ばれる区画が存在している(より小さいメッシュとして4次メッシュ(500m四方), 5次メッシュ(250m四方), 6次メッシュ(125m四方)).

3次メッシュコードは8桁の数値により表現される, 上位4桁が1次メッシュコード, 上位6桁が2次メッシュコードと呼ばれ, より大きなメッシュに対応している. 1次メッシュコードで表現される1区画は緯度差40分, 経度差1度となっている. 日本近辺では１辺の長さが約80kmである. 2次メッシュコードで表現される1区画はは1次メッシュを緯度方向と経度方向にそれぞれ8等分して作られ, 緯度差は5分, 経度差は7分30秒で, 1辺の長さが約10kmに対応する. 3次メッシュコードで表現される1区画は2次メッシュを緯度方向と経度方向にそれぞれ10等分して作られ, 緯度差は30秒, 経度差は45秒であり, 1辺の長さは1kmである.

$(\mbox{緯度},\mbox{経度})=(\mbox{latitude}, \mbox{longitude})$とすると, この緯度と経度の地点が含まれる3次メッシュを表現する地域メッシュコードは以下の式により計算される[1].

\begin{equation}
\mbox{grid square code} = pu qv rw.
\end{equation}

ここで, 整数値$p,u,q,v,r,w$を以下の式で計算する.

\begin{eqnarray}
p &=& \lfloor \mbox{latitude} \times 60 \div 40 \rfloor \quad (\mbox{$p$ is two digits.}),
\\
a &=& \mbox{latitude} \times 60 – p \times 40,
\\
q &=& \lfloor a \div 5 \rfloor \quad (\mbox{$q$ is one digit.}),
\\
b &=& a – q \times 5,
\\
r &=& \lfloor b \times 60 \div 30 \rfloor \quad (\mbox{$r$ is one digit.}),
\\
c &=& b \times 60 – r \times 30,
\\
u &=& \lfloor \mbox{longitude} – 100 \rfloor \quad (\mbox{$u$ is two digits.}),
\\
f &=& \mbox{longitude} – 100 – u,
\\
v &=& \lfloor f \times 60 \div 7.5 \rfloor \quad (\mbox{$v$ is one digit.}),
\\
g &=& f \times 60 – v \times 7.5,
\\
w &=& \lfloor g \times 60 \div 45 \rfloor \quad (\mbox{$w$ is one digit.}),
\\
h &=& g \times 60 – w \times 45,
\end{eqnarray}

また逆に, 3次メッシュコード$pu qv rw$からこのメッシュコードの南西の角の緯度$\mbox{latitude}$と経度$\mbox{longitude}$は次にように計算される.

\begin{equation}
\left\{
\begin{array}{lcl}
\mbox{latitude} &=& p \times 40 \ \div 60 + q \times 5 \div 60 + r \times 30 \div 3600, \\
\mbox{longitude} &=& 100 + u + v \times 7.5 \div 60 + w \times 45 \div 3600.
\end{array}
\right.
\end{equation}

メッシュコードを用いることにより, 日本国内を緯度と経度により区画（メッシュ）に分割し数値列として空間を一意に表現することができる. しかしながら, このメッシュコードは, 日本国内の空間位置に特化した定義であるため, 形式的には, 経度は東経100度から180度, 緯度は北緯0度から66.66度までが定義域となっている(日本の近隣諸国, 例えば, 韓国や台湾ではそのままJIS X0410が利用できるわけであるが, 著者らが知る限り, 日本以外の近隣諸国でJIS X0410を用いた地域メッシュ統計が作成されたことはないようである). そのため, 地球上全ての場所についてメッシュコードが定義できているわけではない. 次節では, JIS X0410を地球全体に拡張する方法について議論する.

3 JIS X0410の世界メッシュコードへの拡張

JIS X0410で標準化されているメッシュコードは日本周辺の場所をうまくメッシュに分割し表現できるように考案されたものであるため, メッシュを定義できる位置$(\mbox{latitude},\mbox{longitude})$の定義域が$0^{\circ} \leq \mbox{latitude} < 66.66^{\circ}$,
$100^{\circ} \leq \mbox{longitude} < 180^{\circ}$と制限されている.

そのため, JIS X0410そのままでは, 日本から遠く離れたの海外の空間を表現するために利用することができない. この問題を克服するために, JIS X0410でのメッシュコードの計算方法を$-90^{\circ} < \mbox{latitude} < 90^{\circ}$, $-180^{\circ} < \mbox{longitude} < 180^{\circ}$に拡張する方法を考えてみよう.

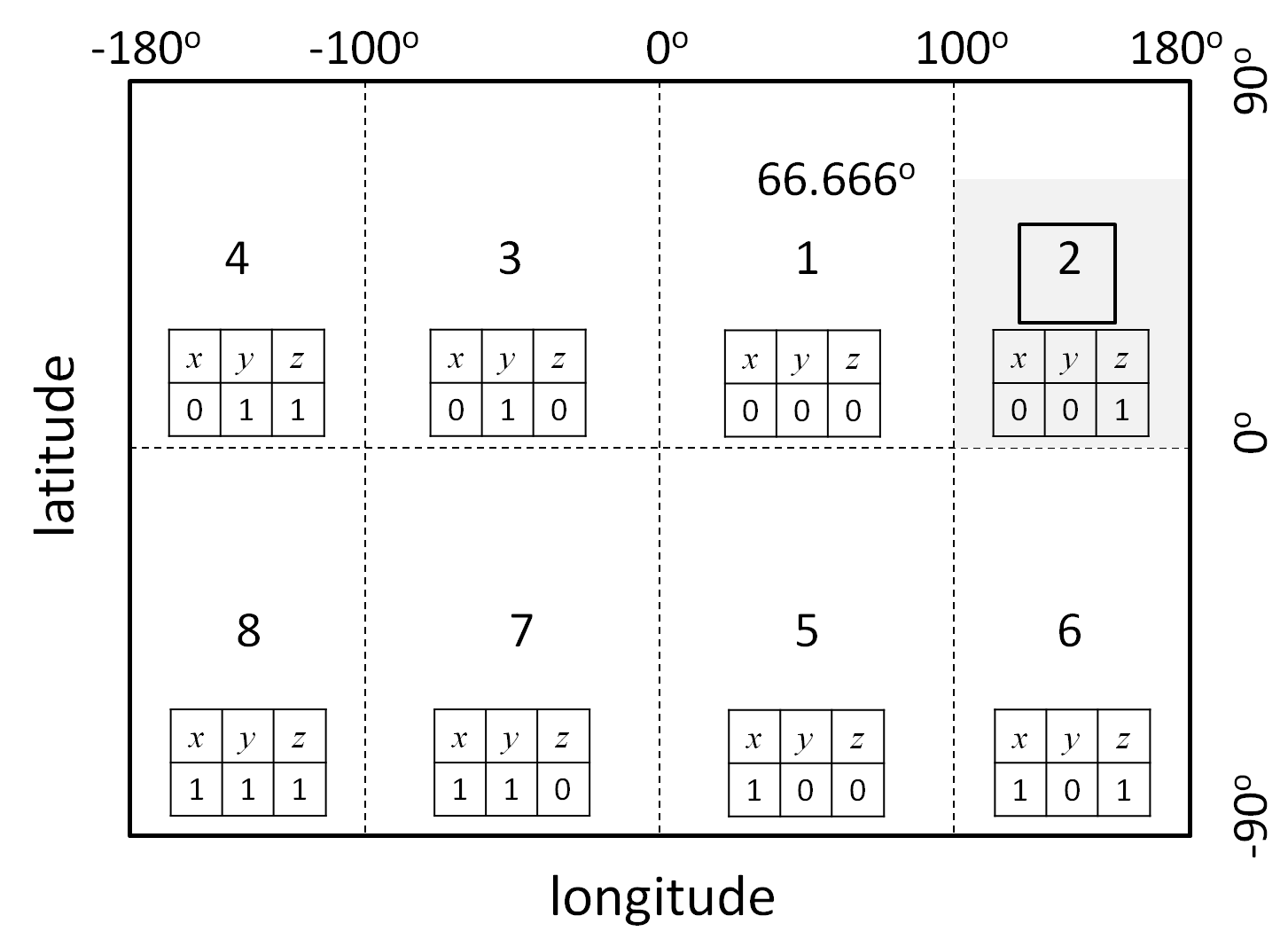
メッシュコードの世界拡張と0次メッシュコードとの関係.

図1に示すように, 世界のすべての場所での緯度と経度の定義域$-90 \leq \mbox{latitude} < 90^{\circ}$, $-180^{\circ} \leq \mbox{longitude} < 180^{\circ}$上でJIS X0410のメッシュコードの定義域$0^{\circ} \leq \mbox{latitude} < 66.66^{\circ}$, $100^{\circ} \leq \mbox{longitude} < 180^{\circ}$となっている場所は斜線の箇所のみである.

$0^{\circ} \leq \mbox{latitude} < 90^{\circ}$, $100^{\circ} \leq \mbox{longitude} < 180^{\circ}$においては, $p$が3桁や1桁となる場合も起こり得るし, $u$が1桁となることもありえる. そのため, まず, １次メッシュコードについて緯度に対応する$p$を2 digitsに制限したものを3 digitsに拡張する. もし, $p$が10未満である場合には, 上位に00を付与して3 digitsとする. $p$が10以上100未満である場合には上位に0を付与して3 digitsとする. また, $u$が10未満の場合にも同様に上位に0を付与して2 digitsとする. 更に, 以下の条件により世界の場所を分割することを考えてみる.

1. 緯度に対しては北緯と南緯の2状態の別を区別する. このために, 北緯($x=0$)と南緯($x=1$)として1bit付与する.
2. 経度に対しては西経と東経の2状態の区別を行う. そのため, 東経($y=0$)と西経($y=1$)として1bitを付与する.
3. 経度の絶対値が100$^{\circ}$未満であるか100$^{\circ}$以上であるかの2状態を区別するために1bitを割り当て, $|\mbox{longitude}| \geq 100^{\circ}$($z=1$)と$|\mbox{longitude}|<100^{\circ}$($z=0$)とする.

このような領域は現状のJIS X0410を含め, すべてで8領域存在している(図1参照). そのため, $xyz$と並べた3ビットを10進数表現としたものに1を加え, 拡張コードとして1 digit(1から8)の数値として割り付ける. この方法を用いることで, 原理的には, JIS X0410の方法でメッシュコードを計算し, 1から8までの拡張コードを1 digitを付与するだけで, 全世界に拡張されたメッシュコードを定義することが可能である. 表1に1から8までの拡張コードに対応する地球上の領域の定義をまとめる. このように定義される1から8までの1 digit 拡張コードを, 便宜上0次メッシュコードと呼ぶことにする.

$xyz$が与えられているとき, 0次メッシュコード$o$の計算方法は,
\begin{equation}
o=2^2 x + 2 y + z + 1.
\end{equation}
となる. 更に, 0次メッシュコード$o$(1～8)が与えられている時, $xyz$は以下で計算できる.
\begin{eqnarray}
z &=& (o – 1) \mbox{ mod } 2, \\
y &=& ((o – z – 1) \div 2) \mbox{ mod } 2, \\
x &=& (o – 2 \times y – z – 1) \div 4,
\end{eqnarray}

位置情報(WGS84)が緯度$\mbox{latitude}$と経度$\mbox{longitude}$で与えられるとき, 各レベルでのメッシュコードの整数値を求める公式は以下のように拡張される.

１次メッシュコード
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0u & (p < 10, u < 10) \\
o0p0u & (10 \leq p < 100, u < 10) \\
op0u & (p \geq 100, u < 10) \\
o00pu & (p < 10, u \geq 10) \\
o0pu & (10 \leq p < 100, u \geq 10) \\
opu & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}

2次メッシュコード
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0uqv & (p < 10, u < 10) \\
o0p0uqv & (10 \leq p < 100, u < 10) \\
op0uqv & (p \geq 100, u < 10) \\
o00puqv & (p < 10, u \geq 10) \\
o0puqv & (10 \leq p < 100, u \geq 10) \\
opuqv & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}

3次メッシュコード
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0uqvrw & (p < 10, u < 10) \\
o0p0uqvrw & (10 \leq p < 100, u < 10) \\
op0uqvrw & (p \geq 100, u < 10) \\
o00puqvrw & (p < 10, u \geq 10) \\
o0puqvrw & (10 \leq p < 100, u \geq 10) \\
opuqvrw & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}

4次メッシュコード
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0uqvrws_2 & (p < 10, u < 10) \\
o0p0uqvrws_2 & (10 \leq p < 100, u < 10) \\
op0uqvrws_2 & (p \geq 100, u < 10) \\
o00puqvrws_2 & (p < 10, u \geq 10) \\
o0puqvrws_2 & (10 \leq p < 100, u \geq 10) \\
opuqvrws_2 & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}

5次メッシュコード
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0uqvrws_2s_4 & (p < 10, u < 10) \\
o0p0uqvrws_2s_4 & (10 \leq p < 100, u < 10) \\
op0uqvrws_2s_4 & (p \geq 100, u < 10) \\
o00puqvrws_2s_4 & (p < 10, u \geq 10) \\
o0puqvrws_2s_4 & (10 \leq p < 100, u \geq 10) \\
opuqvrws_2s_4 & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}

6次メッシュコード
\begin{equation}
\mbox{grid square code} =
\left\{
\begin{array}{ll}
o00p0uqvrws_2s_4s_8 & (p < 10, u < 10) \\
o0p0uqvrws_2s_4s_8 & (10 \leq p < 100, u < 10) \\
op0uqvrws_2s_4s_8 & (p \geq 100, u < 10) \\
o00puqvrws_2s_4s_8 & (p < 10, u \geq 10) \\
o0puqvrws_2s_4s_8 & (10 \leq p < 100, u \geq 10) \\
opuqvrws_2s_4s_8 & (p \geq 100, u \geq 10) \\
\end{array}
\right.,
\end{equation}

ここで, 各整数値は以下で計算される.
\begin{equation}
\left\{
\begin{array}{l}
p: = \lfloor (1-2x)\mbox{latitude} \times 60 \div 40 \rfloor \quad (\mbox{$p$ is two or three digits}),
\\
a := (1-2x)\mbox{latitude} \times 60 – p \times 40, \\
q := \lfloor a \div 5 \rfloor \quad (\mbox{$q$ is one digit}),
\\
b := a – q \times 5,
\\
r := \lfloor b \times 60 \div 30 \rfloor \quad (\mbox{$r$ is one digit}),
\\
c := b \times 60 – r \times 30,
\\
s_{2u} := \lfloor c/15 \rfloor \quad (\mbox{$s_{2u}$ is one digit}),
\\
d := c – s_{2u} \times 15,
\\
s_{4u} := \lfloor d/7.5 \rfloor \quad (\mbox{$s_{4u}$ is one digit}),
\\
e := d – s_{4u} \times 7.5,
\\
s_{8u} := \lfloor e/3.75 \rfloor \quad (\mbox{$s_{8u}$ is one digit}),
\\
u := \lfloor (1-2y)\mbox{longitude} – 100z \rfloor \quad (\mbox{$u$ is one or two digits}),
\\
f := (1-2y)\mbox{longitude} – 100z – u,
\\
v := \lfloor f \times 60 \div 7.5 \rfloor \quad (\mbox{$v$ is one digit}),
\\
g := f \times 60 – v \times 7.5,
\\
w := \lfloor g \times 60 \div 45 \rfloor \quad (\mbox{$w$ is one digit}),
\\
h := g \times 60 – w \times 45,
\\
s_{2l} := \lfloor h/22.5 \rfloor \quad (\mbox{$s_{2l}$ is one digit}),
\\
i := h-s_{2l} \times 22.5,
\\
s_{4l} := \lfloor i/11.25 \rfloor \quad (\mbox{$s_{4l}$ is one digit}),
\\
j := i-s_{4l} \times 11.25,
\\
s_{8l} := \lfloor j/5.625 \rfloor \quad (\mbox{$s_{8l}$ is one digit}),
\\
s_2 := s_{2u} \times 2+s_{2l}+1 \quad (\mbox{$s_{2}$ is one digit}),
\\
s_4 := s_{4u} \times 2+s_{4l}+1 \quad (\mbox{$s_{4}$ is one digit}),
\\
s_8 := s_{8u} \times 2+s_{8l}+1 \quad (\mbox{$s_{8}$ is one digit})
\end{array}
\right..
\end{equation}

逆に, 1次メッシュコード $opu$ ($o$(1 digit), $p$(3 digits), $u$(2 digits))が与えられている場合, その1次メッシュの北西端の位置を表す緯度$\mbox{latitude}$と経度$\mbox{longitude}$は
\begin{eqnarray}
\mbox{latitude} &=& (1-2x) \bigl\{(p-x+1) \times 40 \ \div 60 \bigr\}, \\
\mbox{longitude} &=& (1-2y) (100 \times z + u+y ).
\end{eqnarray}
により計算できる.

2次メッシュコード $opuqv$ ($o$(1 digit), $p$(3 digits), $u$(2 digits), $q$(1 digit), $v$(1 digit))が与えられている場合, その2次メッシュの北西端の位置を表す緯度$\mbox{latitude}$と経度$\mbox{longitude}$は
\begin{eqnarray}
\nonumber
\mbox{latitude} &=& (1-2x) \bigl\{p \times 40 \ \div 60 \\
&+& (q-x+1) \times 5 \div 60 \bigr\}, \\
\label{eq:expression2:latitude-mesh-2}
\mbox{longitude} &=& (1-2y) \bigl(100 \times z + u \\
\nonumber
&+& (v+y) \times 7.5 \div 60 \bigr).
\label{eq:expression2:longitude-mesh-2}
\end{eqnarray}
により計算される.

3次メッシュコード $opuqvrw$ ($o$(1 digit), $p$(3 digits), $u$(2 digits), $q$(1 digit), $v$(1 digit), $r$(1 digit), $w$(1 digit)) が与えられている場合, その3次メッシュの北西端を表す緯度$\mbox{latitude}$と経度$\mbox{longitude}$は
\begin{eqnarray}
\nonumber
\mbox{latitude} &=& (1-2x) \bigl(p \times 40 \ \div 60 + q \times 5 \div
60 \\
&+& (r-x+1) \times 30 \div 3600 \bigr), \\
\label{eq:expression2:latitude-mesh-3}
\nonumber
\mbox{longitude} &=& (1-2y) \bigl(100 \times z + u + v \times 7.5 \div 60
\\
&+& (w+y) \times 45 \div 3600 \bigr).
\label{eq:expression2:longitude-mesh-3}
\end{eqnarray}
により計算できる.

4次メッシュコード $opuqvrws_2$ ($o$(1 digit), $p$(3 digits), $u$(2 digits), $q$(1 digit), $v$(1 digit), $r$(1 digit), $w$(1 digit), $s_2$(1digit)) が得られている場合, その4次メッシュの北西端を表す緯度$\mbox{latitude}$と経度$\mbox{longitude}$は
\begin{eqnarray}
\nonumber
\mbox{latitude} &=& (1-2x) \bigl(p \times 40 \ \div 60 + q \times 5 \div
60 \\
\nonumber
&+& (r-x+1) \times 30 \div 3600 \\
&+& \lfloor (s_2-1)/2 \rfloor + x-1) \times 15 \div 3600 \bigr), \\
\label{eq:expression2:latitude-mesh-4}
\nonumber
\mbox{longitude} &=& (1-2y) \bigl(100 \times z + u + v \times 7.5 \div 60
\\
\nonumber
&+& (w+y) \times 45 \div 3600 \\
&+& (((s_2-1) \mbox{ mod } 2) – y) \times 22.5 \div 3600 \bigr).
\label{eq:expression2:longitude-mesh-4}
\end{eqnarray}
により計算される.

5次メッシュコード $opuqvrws_2s_4$ ($o$(1 digit), $p$(3 digits), $u$(2 digits), $q$(1 digit), $v$(1 digit), $r$(1 digit), $w$(1 digit), $s_2$(1 digit), $s_4$(1 digit))が与えられている場合、その5次メッシュの北西端を表す緯度$\mbox{latitude}$と経度$\mbox{longitude}$は
\begin{eqnarray}
\nonumber
\mbox{latitude} &=& (1-2x) \bigl(p \times 40 \ \div 60 + q \times 5 \div
60 \\
\nonumber
&+& (r-x+1) \times 30 \div 3600 \\
\nonumber
&+& \lfloor (s_2-1)/2 \rfloor + x-1)) \times 15 \div 3600 \\
&+& \lfloor (s_4-1)/2 \rfloor + x-1)) \times 7.5 \div 3600\bigr), \\
\label{eq:expression2:latitude-mesh-5}
\nonumber
\mbox{longitude} &=& (1-2y) \bigl(100 \times z + u + v \times 7.5 \div 60
\\
\nonumber
&+& (w+y) \times 45 \div 3600 \\
\nonumber
&+& (((s_2-1) \mbox{ mod } 2) – y) \times 22.5 \div 3600 \\
&+& (((s_4-1) \mbox{ mod } 2) – y) \times 11.25 \div 3600 \bigr).
\label{eq:expression2:longitude-mesh-5}
\end{eqnarray}
となる.

6次メッシュコード $opuqvrws_2s_4s_8$ ($o$(1 digit), $p$(3 digits), $u$(2 digits), $q$(1 digit), $v$(1 digit), $r$(1 digit), $w$(1 digit), $s_2$(1 digit), $s_4$(1 digit), $s_8$(1 digit)) が与えられている場合、その6次メッシュの北西端を表す緯度$\mbox{latitude}$と経度$\mbox{longitude}$は
\begin{eqnarray}
\nonumber
\mbox{latitude} &=& (1-2x) \bigl(p \times 40 \ \div 60 + q \times 5 \div
60 \\
\nonumber
&+& (r-x+1) \times 30 \div 3600 \\
\nonumber
&+& \lfloor (s_2-1)/2 \rfloor + x-1)) \times 15 \div 3600 \\
\nonumber
&+& \lfloor (s_4-1)/2 \rfloor + x-1)) \times 7.5 \div 3600 \\
&+& \lfloor (s_8-1)/2 \rfloor + x-1)) \times 3.75 \div 3600 \bigr), \\
\label{eq:expression2:latitude-mesh-6}
\nonumber
\mbox{longitude} &=& (1-2y) \bigl(100 \times z + u + v \times 7.5 \div 60
\\
\nonumber
&+& (w+y) \times 45 \div 3600 \\
\nonumber
&+& (((s_2-1) \mbox{ mod } 2) – y) \times 22.5 \div 3600 \\
\nonumber
&+& (((s_4-1) \mbox{ mod } 2) – y) \times 11.25 \div 3600 \\
&+& (((s_8-1) \mbox{ mod } 2) – y) \times 5.625 \div 3600 \bigr).
\label{eq:expression2:longitude-mesh-6}
\end{eqnarray}
となる.

JIS X0410を世界拡張するための拡張コード(0次メッシュコード)の定義.

$x$: 緯度$y$: 経度$z$: 経度の範囲$x|y|z$10進数表現
$0$: 北緯 ($\mbox{latitude} > 0^{\circ}$)$0$: 東経 ($\mbox{longitude} > 0^{\circ}$)$0$: $|\mbox{longitude}| < 100^{\circ}$$0|0|0$$1$
$0$: 北緯 ($\mbox{latitude} > 0^{\circ}$)$0$: 東経 ($\mbox{longitude} > 0^{\circ}$)$1$: $|\mbox{longitude}| \geq 100^{\circ}$$0|0|1$$2$
$0$: 北緯 ($\mbox{latitude} > 0^{\circ}$)$1$: 西経 ($\mbox{longitude} < 0^{\circ}$)$0$: $|\mbox{longitude}| < 100^{\circ}$$0|1|0$$3$
$0$: 北緯 ($\mbox{latitude} > 0^{\circ}$)$1$: 西経 ($\mbox{longitude} < 0^{\circ}$)$1$: $|\mbox{longitude}| \geq 100^{\circ}$$0|1|1$$4$
$1$: 南緯 ($\mbox{latitude} < 0^{\circ}$)$0$: 東経 ($\mbox{longitude} > 0^{\circ}$)$0$: $|\mbox{longitude}| < 100^{\circ}$$1|0|0$$5$
$1$: 南緯 ($\mbox{latitude} < 0^{\circ}$)$0$: 東経 ($\mbox{longitude} > 0^{\circ}$)$1$: $|\mbox{longitude}| \geq 100^{\circ}$$1|0|1$$6$
$1$: 南緯 ($\mbox{latitude} < 0^{\circ}$)$1$: 西経 ($\mbox{longitude} < 0^{\circ}$)$0$: $|\mbox{longitude}| < 100^{\circ}$$1|1|0$$7$
$1$: 南緯 ($\mbox{latitude} < 0^{\circ}$)$1$: 西経 ($\mbox{longitude} < 0^{\circ}$)$1$: $|\mbox{longitude}| \geq 100^{\circ}$$1|1|1$$8$

このように定義すると, これまでJIS X0410で定義されていたメッシュコードの最上位に0次メッシュコード2と1次メッシュコードの先頭に0を付与するだけで, 世界拡張されたメッシュコードとすることができることがわかる. すなわちJIS X0410から計算されるメッシュコードの先頭に20をつけることで世界拡張されたメッシュコードに読み替えすることができる.

ここで紹介した著者らが提案する世界メッシュコードの試案をR言語により実装し公開している[10]. このライブラリでは以下の関数が定義されている.

  • 世界3次メッシュの4隅の緯度と経度を出力する
meshcode_to_latlong_grid(meshcode)
  • 世界3次メッシュの北西端における緯度と経度を出力する
meshcode_to_latlong_NW(meshcode)
  • 世界3次メッシュの南西端における緯度と経度を出力する
meshcode_to_latlong_SW(meshcode)
  • 世界3次メッシュの北東端における緯度と経度を出力する
meshcode_to_latlong_NE(meshcode)
  • 世界3次メッシュの南東端における緯度と経度を出力する
meshcode_to_latlong_SE(meshcode)
  • 位置情報（緯度と経度）からその位置が含まれる世界3次メッシュコードを出力する
cal_meshcode(latitude,longitude)

地球はおおよそ半径$r$が6,371kmの球型をしていることから, その表面積$S$は$S = 510,100,000$ km$^2$程度である. 全球に渡る1次メッシュの総数は 360 $\times$ 180 $\times$ 3/2 = 97,200となる. 2次メッシュの総数は1次メッシュの64倍であるので, 全球に渡る2次メッシュの総数は 6,220,800 となる. 3次メッシュの総数は2次メッシュの総数の100倍であるので, 全球に渡る3次メッシュの総数は 622,080,000 である. 4次メッシュの総数は3次メッシュの4倍であるため, 4次メッシュの総数は 2,488,320,000 となる. 5次メッシュの総数は更に4次メッシュの4倍であるので, 5次メッシュの総数は 9,953,280,000 である. 6次メッシュの総数は 5次メッシュの総数の更に4倍であるので, 6次メッシュの総数は 39,813,120,000 となる.

また, 地球上における陸域面積は全球の 29.1998% を占めているため, 各レベルにおける世界メッシュの総数と陸域における世界メッシュの総数はそれぞれ以下の表のようになる.


全球に渡る世界メッシュの総数と陸域における世界メッシュの総数.
世界メッシュレベル全球に渡るメッシュ総数陸域におけるメッシュ総数
1次メッシュ97,20028,383
2次メッシュ6,220,8002,838,220
3次メッシュ622,080,000181,646,116
4次メッシュ2,488,320,000726,584,463
5次メッシュ9,953,280,0002,906,337,853
6次メッシュ39,813,120,00011,625,351,413

4 提案手法と競合する可能性のある他方法との比較

ここでは, 今回試案として提案するJIS X0410の拡張による世界メッシュコードの拡張と競合する可能性のある, 他国異分野におけるグリッド定義法を概観し, それらの長所と短所について調べてみる.

世界的なメッシュコードの決定方法については, 緯度経度と対応させる代わりに等面積性を犠牲とする方法と, 逆に等面積性を保証するかわりに緯度経度との対応を失う２つの方向性が存在している. 代表的には, 前者が日本の規格, 後者がイギリスの規格である.

4.1 The U.S. Military Grid Reference System (MGRS)

The U.S. Military Grid Reference System (MGRS)は1940年代にUnited States Army Corps of Engineersにより開発されたグリッド構成方法である. ユニバーサル横メルカトル図法に基づき緯度方向に8度ごとに南緯80度から北緯72度まで20のゾーンに分割し, 経度方向に西経180度から東経180度まで6度ずつ60ゾーンに分割し, 緯度方向に北からCからXの符号を, 経度方向に西から1から60の数字を割付てこの組合せにより100km四方のグリッドを表現する仕組みを有する.

この方法は国土地理院において, 昭和40年代から25,000分の1地形図整備に合わせて採用されるようになった（日本では, 51帯～56帯を使用）(http://www.gsi.go.jp/chubu/minichishiki10.html　国土地理院ではUTMグリッド地図として利用が試みられている). メッシュを等面積で構成できる利点がある. ゾーンとメートル単位の直交座標系を使って地球上の位置指定を行うことができる長所を有する. ただし, ゾーン間で不連続接続が存在するという問題がある. また, ゾーンが南緯80度から北緯72度までと制限が存在している. 世界的に見て統計目的での利用例はあまりない.

4.2 Ordnance Survey National Grid reference system

イギリスにおいて利用されている地域グリッド参照システムであり, 元来はイギリス測地系OSGB36に基づく北緯49度西経2度を原点とするユニバーサル横メルカトル図法により基準線を決定する. 測地系によりETRS89あるいはOSTN02に基づくものに修正がなされてきた経緯がある. アルファベット１文字により500km四方の縦横5グリッドづつにユニバーサル横メルカトル図法に基づき25個のグリッドとしてイギリス領内を分割している. 更に, 各グリッドは100km四方に25個の分割されそれぞれは2文字のアルファベットの組合せとしてイギリス領内を表現するために利用される. また, 100km四方は100個の10km四方のグリッドに分割されアルファベット２文字と数字2桁により表示される. 各10km四方のグリッドが更に100分割されアルファベット2文字と数字4桁からなる1kmグリッドとなる. イギリスではメッシュ統計作成にOrdnance Survey National Grid reference systemが利用されており, ユニバーサル横メルカトル図法に基づくためメッシュを等面積で構成できる利点がある.

英国におけるグリッドの導入の歴史は1919年に英国軍により導入されたBritish Grid Systemに遡る[11]. その後, 1927年にModified British Systemに改良され利用され続けた. 1929年1メッシュ5000ヤードの規格が制定され, 1インチの地図に使用されるようになった. 1931年から一般にメッシュ統計として利用されるようになった. 1938年のDavidson Committee Reportにおいて実験データにグリッドが使われた記録がある. その後メートル世界基準が導入されるにともない現在のメートル表記に改訂され英国全土を覆うグリッド規格へと成長してきた. 但し, ユニバーサル横メルカトル図法を用いているため, 世界全体を覆う場合, 原点から遠ざかるにつれてグリッドの歪みが緯度経度から見て大きくなるという問題がある. この歪みを避けるために複数の原点の異なる投射を用いると, 原点の異なるグリッド間に隙間を生じてしまう問題がある. そのため, イギリス全土を覆うメッシュ定義方法としては大変優れているが, 世界全体を覆うメッシュ定義法として利用しようとすると, いくつかの克服すべき問題を有する.

ISO(TC211)は空間データ, メタデータ, 座標による空間参照, 画像とグリッドデータ, およびデータ品質について取り扱っている. BSI (British Standards Institution)ではBS7567(aka NTF)とBS7666(空間データセットと地理参照)において地理データを取り扱っている. 更に, Ordnance SurveyはIST/36においてBSIのメンバーになっており, 地理情報の分野において国際委員会にUKメンバーとして参加している.

4.3 European statistical grid

European gridは多目的な全欧州地図標準でありETRS89 Lambert Azimuthal Equal-Area projection coordinate reference system （投射中心は北緯52度, 東経10度）x0=4321000m yo=3210000m (ETRS89-LAEA)に基づく. このグリッド定義を特にETRS89-LAEA5210と呼ぶ. グリッド解像度は1m, 10m, 100m 1000m, 10,000m, 100,000m　と階層的になっており, グリッドの構成は南北, 東西である. 1kmグリッドは1kmN????E????と南北方向に４桁, 東西方向に４桁の数字を割り振ることによりメッシュを参照する.

ETRS89-LAEAは2003年に提唱され, 現在Eurostatなどが導入を始めている. ETRS89-LAEAの仕様とコーディング方法については, EUR Report 21494 EN:39-46[13]の勧告に基づき設計がなされた. 勧告の骨子は以下のようになっている.

  • 簡単に取り扱える
  • 階層的な構造をもつ
  • 欧州で共通のグリッドを定義する
  • 面積が一定で等しい
  • ETRS-LAEAを採用する
  • タイムスタンプを取り扱える
  • ISO19113-11915にしたがうデータ品質原理にしたがう
  • Grid Data Modelは完全に文章公開される
  • グリッドデータの転送は被独占的オープンフォーマットにより行う
  • メタデータ（ISO準拠)が生成でき, 定期的に更新されなければならない.

これらの勧告にしたがいETRS89-LAEAは現在欧州全体において利用できるよう整備さ進められている. http://spatialreference.org/ref/epsg/etrs89-etrs-laea/からメッシュコードの仕様とコーディング方法を参照することができる.

ETRS89-LAEAに基づくオープンデータとしてEurostatが公開しているものがある. 代表的なデータとして2006年Pan Europaにおける人口グリッドデータ[14]がある.

この方法では投射点の選び方を複数変えながら世界を覆うことにより, 適切な投射点を地球上に選択し, いくつかの場所に分割することにより世界を等面積により覆うメッシュを構成することが可能である. 但し近接するメッシュでは方向や向きが異なるため接続点近傍での不一致が発生する問題がある.

4.4 グリッド・ロケイター（GL)

世界規模でのグリッド定義方法として, アマチュア無線の分野では無線局の位置を特定する目的で, グリッド・ロケーター(GL)と呼ばれる階層的なメッシュ定義による位置表記方法が使われている. この方法は, JIS X0410に類似した方法で, アルファベット2文字, 数字2桁, アルファベット2文字の合計6文字で世界中の18,662,400サブエリアを特定する方法である. GLはヨーロッパのアマチュア無線で提唱され現在広くアマチュア無線局の位置を指示する記号として利用されている.

GLでは世界を緯度と経度により$18\times 18$の324フィールドに分割しこれを2文字のアルファベットにより表現する. 更に各フィールドは$10\times 10$に100分割され$01$から$99$までの数が割り当てられる. 南西角が01でそこから北方向に$02, 03, 04 \ldots$となる. 北西の角まできたら次は東に1スクエア進めて$10, 11, 12, \ldots$と番号をつける. 各スクエアは$24\times 24$に576に分割され, アルファベッと2文字により表現されるサブスクエアを定義する. 全世界は$324,00 \times 576=18,662,400$のサブスクエアにより構成される.

最終的に, サブスクエアはアルファベット2文字, 数字2文字, アルファベット2文字の6文字を用いて世界のすべてのサブスクエアを一意に表現することが可能である. この方法は, 主として世界のアマチュア無線局の場所を表現する目的でのみ利用されており, 統計目的での利用実績は存在していない.

4.5 比較結果

JIS X0410は世界的に見ると緯度経度との対応を保つかわりに等面積性を犠牲とすることを基本的な理念としており, イギリスで広く用いられているOrdnance Survey National Grid reference system[11]やEuropean grid[13]で採用されている等面積性を保つことに注力している方法とは異なる方向性となっている. 統計利用には面積一定とするMGRS, Ordnance Survey National Grid reference system, European gridの方が優れているよう思われる. 一方で, 日本のJIS X0410で規程されているメッシュコードは緯度経度に基づくもので全てのグリッドの面積は正確に一致しているものとなっていないが, 近似的におおよそ等しく, また緯度と経度と対応するため理解が容易であるという利点がある.

NOAAは地球上の各位置（緯度と経度）での標高データの作成を行い世界を全てカバーするグリッドデータを作成し提供しているが[14], このような目的では緯度経度を用いたグリッド定義方法のほうが優れている.

等面積性を保つメッシュ定義方法とJIS X0410のような緯度経度に対応させてメッシュコードを規程する方法についてはどちらも一長一短があり, 利用目的によって使い分ける必要がある.

こと, 世界全体を覆うことを目的とする場合, 等面積性を保つメッシュ定義方法では投射点を必要とするため, 投射点から遠く離れるにつれてメッシュの実際の形状が格子から歪むという欠点がある. また, 複数の投射点をもつ異なるメッシュで被覆しようとした場合, メッシュ間で隙間を生じてしまうという問題もある. そのため, 緯度と経度と単純に対応するメッシュ定義方法のほうが世界全体を覆うメッシュ定義方法としては優れている. 面積がメッシュにより異なるという問題点は, メッシュごとの面積のメッシュ統計を作成することにより, 単位面積当たりの計算を行う目的であれば解決することが可能である.

5 世界メッシュコードの利活用の可能性

世界メッシュコードの利用価値としていくつかの利用可能性について考察してみる.

地域メッシュ統計は国土の様子を把握する上で有効な方法であるが, 区画を定義する必要があることから, この区画定義を国家的に果たすことができた国においてのみ作成, 利用することが現在できている.

この背景を勘案して, まず一つ目に発展途上国における公的統計にメッシュ統計を容易に導入するために提案した世界メッシュを利用する方向性が考えられる. 近年のGPSの普及により, 地球上のあらゆる場所においてGPSを用いた緯度と経度の決定が可能となっている. このような位置情報を測位するデバイスに世界メッシュ変換機能を持たせることにより, 発展途上国においても統計作成時にメッシュコードを付与した統計集計方法を確立することができる可能性がある. 更に, 住所が未定義の場所においてもこの方法を用いることにより統計を作成することが可能である.

二つめの利用方法として, 既存のWebサービス上でリアルタイムメッシュ統計を利用する方法が考えられる. 現在Webアプリケーションでは, 位置情報付きのマッシュアップサービス等が普及し, 広く利用できるようになってきている. このように収集, 利用される位置情報付きのデータを用いることにより, 店舗や公共施設, 人に移動情報などのメッシュ統計を世界規模で作成することが可能である. この様に作成したメッシュ統計を国や地域の境界情報が組み込まれたメッシュを用いてフィルターし, 峻別集計することにより, 各国の公的統計に頼ることなく, 全世界規模での国別, 地域別統計を網羅的に作成することが可能と思われる.

三つめの利用方法として, IoTとの組み合わせが考えられる. IoTにおいては位置情報を利用したアプリケーションが考えられているが, 個人情報保護の観点から位置情報を直接サーバーに送信することに抵抗があることがほとんどである. そのため, 位置情報をサーバーに送信する代わりに世界メッシュコードを送信することにより, 位置の秘匿がある程度可能となる. 更に, 世界メッシュコードを利用して集められたセンサー情報やモバイル端末からの情報を集計することにより, リアルタイム性の高いメッシュ統計（リアルタイムメッシュ統計）を生成し, 個人情報を秘匿しつつ, 現状をリアルタイムで把握し, 共有する方法へと拡張が可能である. このような方法を用いることにより, 利用したいサービスや商品が存在している場所へと人々を誘導するサービスや, 空間検索を高速に行うアルゴリズムの開発に利用可能である.

このような背景から, 世界メッシュコードは公共性が極めて高く, 個人や一部の企業が独占すべきではなく, 世界標準規格として広く世界の公共の財産として利用されるべきである. 世界標準規格としてISO TC69(統計的方法の適用専門委員会)およびISO TC 211(地理情報専門委員会)双方の作業により, 日本産業規格を拡張して世界標準規格とすることができれば, 今後ビッグデータ時代における世界的な標準として多くの産業を生み出す可能性が考えられる.

6 まとめ

本稿では, メッシュ統計を作成する上でなくてはならない, 地域メッシュコード(JIS X0410)を世界全体に拡張する方法について論じた. この方法を用いることにより, 世界約5億1千万の約1km四方の区画を一意に10桁の数列により表現することが可能である.

JIS X0410は1976年に日本工業規格（現日本産業規格）として認定されて以来, 我が国は地域メッシュ統計では長い歴史と実績を有している. 我が国は世界に先駆けて地域メッシュ統計を作り上げてきた実績を有していると言える．そして, 来年2016年は地域メッシュコードがJIS X0410として日本工業規格（現日本産業規格）として標準化がなされて以来、40周年の節目の年となる.

この長い歴史を有する日本の地域メッシュ統計に関する我が国の標準規格が世界標準規格のもととなることは, 世界に日本の歴史ある統計利用方法を普及させ, ビッグデータ時代におけるリーダーシップを発揮できる契機となり得る. 更に, 日本の40年間の歴史で培ってきた多くの人的, ハード的資源を世界標準規格の枠組みの中で保護し, 我が国で蓄積してきた地域メッシュ統計を永続的に利用することを可能とする国益に叶う施策となり得る.

謝辞

本稿を作成するに当たり, 総務省統計局統計調査部調査企画課地理情報室には大変お世話になった. ここに感謝の意を示す. 本研究の一部は国立研究開発法人科学技術振興機構(JST)の戦略的創造研究推進事業(さきがけ)の支援によって行われている.

[1] 総務省統計局 地域メッシュ統計の概要 [10 August 2015] http://www.stat.go.jp/data/mesh/gaiyou.htm
[2] e-Stat https://www.e-stat.go.jp/SG1/estat/eStatTopPortal.do
[3] 地図で見る統計（統計GIS）https://www.e-stat.go.jp/SG1/estat/toukeiChiri.do?method=init
[4] 国土交通省国土政策局国土情報課 http://www.mlit.go.jp/kokudoseisaku/kokudojoho.html
[5] 佐藤彰洋, 椿広計, ビッグデータ時代に必要な標準化, 統計, 2015年9月号, pp.32–38.
[6] 国土実態総合統計の開発・整備に関する研究報告（昭和46年）発行：総理府統計局
[7] 国土交通省観光庁 http://www.mlit.go.jp/kankocho/
[8] 宿泊旅行統計調査 http://www.mlit.go.jp/kankocho/siryou/toukei/shukuhakutoukei.html
[9] 世界メッシュコードの計算用ライブラリを以下URLで公開している. https://www.fttsus.jp/worldgrids/libraries/
[10] Ordnance Survey National Grid reference system http://www.ordnancesurvey.co.uk/support/the-national-grid.html
[11] Ordnance Survey http://www.ordnancesurvey.co.uk/support/understanding-gis/standards.html
[12] EUR Report 21494 EN:39-46 http://www.ec-gis.org/sdi/publist/pdfs/annoni2005eurgrids.pdf
[13] GEOSTAT_Grid_POP_2006_1K http://www.efgs.info/data/geostat/open-data
[14] Amante, C. and B.W. Eakins, 2009. ETOPO1 1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis. NOAA Technical Memorandum NESDIS NGDC-24. National Geophysical Data Center, NOAA. doi:10.7289/V5C8276M Accessed on 13 May 2013.